Quantum Superposition

Every physical quantity has a Hermitian operator associated with it and the linear combination of the eigenstates of this operator gives us Quantum Superposition.

The concept of superposition can be best understood by examples.

Let’s consider a thought experiment (this experiment is very similar to the Stern–Gerlach experiment except the fact that we will consider neutrons instead of silver atoms). Let’s say you have a number of neutrons. Let’s take 2 characteristics of neutrons : color (green or blue) and shape (circular or rectangular). Now consider 2 different detectors - one for shape and the other for color. Now we direct neutrons towards the color detector and we find that we get 50% blue and 50% green. Now we direct the neutrons to the shape detector and find that again there is a 50% probability for both circular and rectangular shapes. Now we take different combinations and find what percentage of blue neutrons turn out circular, what percent of green neutrons turn out rectangular, what percent of circular neutrons turn out green, and what percent of rectangular neutrons turn out blue. After finding the results of these combinations, we find that in all the cases the probability is 50%.

Now we will take the neutrons direct them towards a shape detector and take the circular neutrons and direct them towards a color detector and then take the green ones and direct them through a shape detector again. What do you think we will find? We find that the probability is still 50%.

Now we take the neutrons through a color detector from where the green neutrons are taken to the shape detector and here the neutrons are sorted between rectangle and circle. Then the rectangular neutrons are directed towards a mirror which directs them toward a beam splitter, same is the case with the circular neutrons. Now from the beam splitter, the neutrons go to a color detector. Now, interestingly, the probability of green neutrons is 100%.

Let’s do this experiment again and this time block one of the paths of neutrons (for example circular neutrons). In this case we find that the probability again comes out to be 50%.

So we can conclude that at one particular point of time we can only know any one characteristic property of neutrons, either the shape or the color. In the 1st experiment we knew the shape but not the color, in the 2nd experiment we knew the color but not the shape, and in 3rd we knew the shape but not the color.

The neutron was in a superposition of being square and circular at the same time, and we can’t know both the shape and the color at the same time. But in fact the neutron doesn’t have a shape and color at the same time. Having a definite shape means not having a definite color and vice-versa.

Let’s move on to the next experiment now

We all have heard about the famous Schrödinger Equation. What does it tell us? It tells us about the wavefunction of a particular particle or system.

Now we let’s look at Schrodinger’s cat experiment.

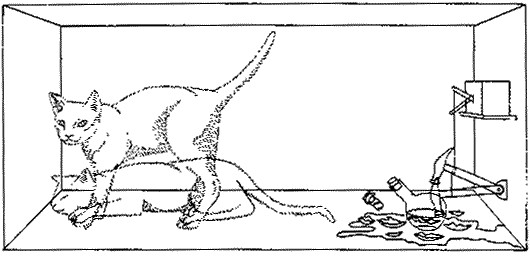
Let’s consider a box having a cat inside it along with radioactive substance. The box also has a radiation detector which will detect if the radioactive substance has decayed or not. If it detects any radiation then a flask containing poison will break, thereby killing the cat. Consider this entire apparatus as a quantum system. Now the probability that the cat will die or will not die (as a result of decay taking place or not taking place) will be in superposition.

Hence we can conclude that the quantum state of the system will be the following:-

This expression may seem intimidating to some of you; however, it simply signifies that there exists a uniform superposition of the |0> and  |1> state.

The measurement of the state of the system forces the system to be in either the |0>  state or the |1>  state with an equal probability. Measurement means when we finally open the box to check if the cat is dead or alive. As soon as we open the box we find that there is only one outcome and both the outcomes have an equal probability.

I hope I didn’t bore you and that you understood this. Stay tuned for my next article on superposition.

Spoiler Alert :- It will include Quantum Computing